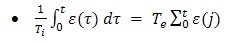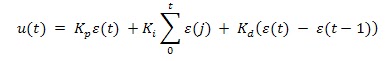Présentation
L’objectif de l’asservissement PID (Proportionnel Intégral Dérivé) est de stabiliser le système en
fonction d’une consigne. On cherche à atteindre une position donnée dans le cas du chariot, en traitant l'erreur entre la consigne et la mesure fournit par le capteur par le contrôleur PID, la nouvelle valeur obtenue sert de commande pour le moteur. On aura donc compris que la commande joue simplement sur la vitesse du moteur à travers le PWM.
Structure d'une boucle d'asservissement:
Ce modèle est une structure en parallèle mais il
existe plusieurs architectures de PID, en série ou mixte.
Il y a trois paramètres à régler:
- L’action proportionnel P: amplifie l’erreur d’un
facteur Kp (le gain) permettant une réaction plus rapide du système au
changement de consigne en fonction du gain, mais peut faire diverger le système
si celui-ci est trop élevé.
- L’action intégrale I: pour compenser l’erreur statique
que l’action proportionnelle ne peut pas prendre en charge, l’action intégrale
intègre cette erreur pendant un temps Ti, le résultat est ensuite ajouté à la commande. Plus cette action est
importante, plus les oscillations autour de la consigne seront accentuées.
- L’action dérivé D: cette action dérive l’erreur
pendant un temps Td, cela permet de diminuer les dépassements et le temps
de stabilisation mais est très sensible au bruit.
Un peu de mathématiques pour déterminer l'algorithme du PID numérique
Les calculs suivants traiteront de la forme parallèle du contrôleur PID comme on vient de voir. Il peut paraître fastidieux, j'ai donc essayé de simplifier. Ce qu'il faut vraiment retenir c'est le résultat final et la signification de chaque terme de l'équation.
Pour un contrôleur PID parallèle, l'équation à temps continu s’écrit:
u(t) et ε(t) représentent respectivement le signal de commande et d’erreur à l’instant t. K est
le gain proportionnel, Ti
le temps d’intégration et Td
le temps de dérivation.
A temps discret
l’intégrale et la dérivée deviennent:
Te
est la période d’échantillonnage.
D’où l’équation
du PID à temps discret:
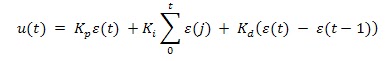
Ce qui
permet de définir les paramètres Kp,
Ki et Kd en fonction de la période d’échantillonnage:
Maintenant revenons
sur l’équation du début à temps continu. Sa transformée de Laplace s'écrit:
L’équivalent à temps discret de la
transformée de Laplace est la transformée en Z, ce qui nous donne:
Si on prend en compte les paramètres Kp
, Ki et Kd décrits précédemment on aura donc:
En réarrangeant:
Ou encore:
Avec
En mettant sous la forme
d’'une équation aux différences on obtient:
u[k] est la valeur de la commande à l'instant k, elle est calculée en fonction des valeurs de commande et d'erreur à des instants passés représentés par k-1 et k-2.
Cette forme d’équation devient alors facilement
implémentable en logique programmable par l'utilisation de bascule D, multiplieurs et additionneurs.
Schéma bloc du contrôleur PID parallèle numérique:
Programme VHDL
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.NUMERIC_STD.ALL;
entity PID_simple is
port( clk : in std_logic;
set_point : in signed(15 downto 0); --signal de commande
measure : in signed(15 downto 0); --signal de control
K1,K2,K3 : signed(7 downto 0) := (others => '0'); --parametre PID
PIDout : inout signed(23 downto 0)); --sortie asservissement
end PID_simple;
architecture behavior of PID_simple is
signal error_prev1, error_prev2, error : signed(15 downto 0) := (others => '0');
signal u_prev, add_out : signed(23 downto 0) := (others => '0');
begin
error <= set_point - measure; --calcul de l erreur
add_out <= u_prev + K1*error + K2*error_prev1 + K3*error_prev2; --equation aux differences
process(clk) --retard
begin
if(rising_edge(Clk)) then
error_prev1 <= error;
error_prev2 <= error_prev1;
u_prev <= add_out;
PIDout <= add_out;
end if;
end process;
end behavior;